
인공지능 및 기계학습 개론 2(7.7~7.9) 정리
Dobby-HJ
·2023. 10. 9. 18:53
7.7 Variable Elimination
Marginalization and Elimination
- Computing joint probabilities is a key
- How to compute them?
- Many, many, many multiplications and summations
- $P(a=ture, b=ture, mc=ture) = \sum_{jc}\sum_{E}P(a,b,E,JC, mc)
\= \sum_{JC}\sum_E P(JC|a)P(mc|a)P(a|b,E)P(E)P(b)$- 기억이 안나서 메모하자면, marginalization하는 과정은 쉽게 생각해서 hidden variable의 모든 상태(?)대해서 summation하면 되고, $P(a,b,E,JC, mc)$가 아래처럼 바뀐 이유는 graphical한 의존관계를 이용해 Factorization했기 때문.
- $P(a=ture, b=ture, mc=ture) = \sum_{jc}\sum_{E}P(a,b,E,JC, mc)
- In big Oh notation?
- Is there any better method?
- What-if we move around the summation?
- $P(a,b,mc) = \sum_{JC}\sum_E P(a,b,E,JC, mc)\
= P(b)P(mc|a)\sum_{JC}P(JC|a) \sum_E P(a|b, E)P(E)$
- $P(a,b,mc) = \sum_{JC}\sum_E P(a,b,E,JC, mc)\
- Did we reduced the computation complexity?
- What-if we move around the summation?
Variable Elimination
- Preliminary
- $P(e|jc, mc) = \alpha P(e, jc, mc)$ → 여기서 $\alpha$는 normalize constant의 느낌으로 동작하지만, 계산을 하면 joint probability를 구할 때(베이즈 정리)를 사용한다면 $\frac{1}{P(jc, mc)}$로 계산됩니다.
- Joint probability(e=jc=çΩ
- $P(e, jc, mc, B,A) = \
\alpha P(e)\sum_B P(b) \sum_A P(a|b,e)P(jc|a)P(mc|a)$- Line up the terms by the topological order → graphical한 정보에 의해서 위장 정렬 순으로 항을 정렬해서 나타내보겠다.(e → b → a → jc → mc)
- Consider a probability distribution as a function
- $f_e(E=t) = 0.002$
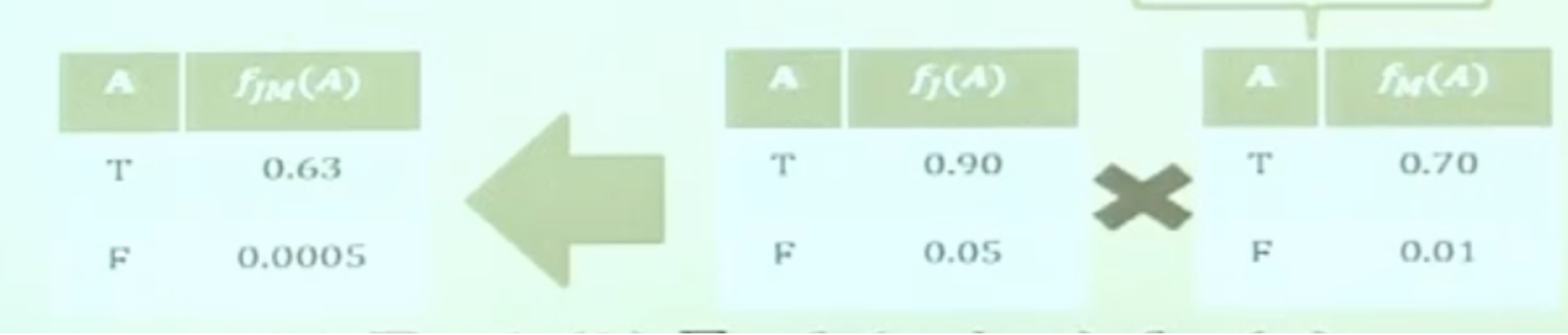
- $=\alpha f_E(e)\sum_Bf_B(b)\sum_Af_A(a,b,e)f_J(a)f_M(a)$
→ 여기서 $P(jc|a)P(mc|a) \rightarrow f_J(a)f_M(a)$으로 수정되었는데, 이유는 같은 $a$를 condition으로 하는 function으로 생각할 수 있음 그래서 $a$의 condition을 parameter로 하는 2개의 function으로 나눈뒤, 둘다 같은 parameter에 대한 곱으로 계산하는 것이므로 table에서 보면 단순 곱의 형태로 나타낼 수 있다.
- $P(e, jc, mc, B,A) = \
7.8 Potential Function and Clique Graph
Potential Functions
- $P(A,B,C,D)$
- $= P(A|B)P(B|C)P(C|D)P(D)$
- Let’s define a potential function
- Potential function :
a function which is not a probability function yet, but once normalized it can be a probability distribution function
→ 아직 몇 가지의 특성이 만족이 되지 않아 PDF(Probability Distribution Function)이 되지 않은 함수. 하지만 의미론적으로 유사해서 확률을 해석할 때처럼 사용하는 함수처럼 생각하는 듯 - Potential function on nodes
- $\psi(a, b), \psi(b, c), \psi(c, d)$
- Potential function on links
- $\phi(b), \phi(c)$
- How to setup the function?
- $P(A,B,C,D) = P(U) = \frac{\Pi_N \psi(N)}{\Pi_L\phi(L)} = \frac{\psi(a, b), \psi(b, c), \psi(c, d)}{\phi(b), \phi(c)}$
- → 모든 Potential Function을 곱한 것에 모든 Seperator Function을 나눈 것으로 정의할 수 있음.*
- $\psi(a,b) = P(A|B),\ \psi(b,c) = P(B|C),\ \psi(C,D) = P(C|D)P(D)$
- $\phi(b) = 1, \phi(c) = 1$
- 위의 $\psi$ function을 위와 같이 나타내면 처음의 $P(A,B,C,D)$의 graphical한 성질은 띄우면서도 만족할 수 있습니다.(다만, 현재는 우리가 위와 같이 정의를 했기 때문에 가능한 것 같습니다.)
- $P(A,B,C,D) = P(U) = \frac{\Pi_N \psi(N)}{\Pi_L\phi(L)} = \frac{\psi^(a, b), \psi^(b, c), \psi^(c, d)}{\phi^(b), \phi^*(c)}$
- $\psi^(a,b) = P(A|B),\ \psi^(b,c) = P(B|C),\ \psi^*(C,D) = P(C|D)$
- $\phi^(b) = P(B), \phi^(c) = P(C)$
- 이렇게도 joint probability를 $\psi$로 정의해서 일반화도 가능한 것 처럼 보입니다.
- Potential function :
- Marginalization is also applicable
- $\psi(w) = \sum_{v-w}\psi(v)$
- Constructing a potential of a subset (w) of all variables(v)
- 아래의 그림에서 $A$ ← $B$ ← $C$ ← $D$인 directed graph가 있을 때 이를 Clique와 Separator로 구분해서 그리게 되면 아래 그림처럼 나오게 됩니다. Clique는 undirected graph에서 적용되는 자료구조로, 각 원소들이 Fully-connected되어 있으면 해당 sub graph는 Clique라고 합니다.

Absorption in Clique Graph
- Only applicable to the tree structure of clique graph
- Let’s assume
- $P(B) = \sum_A \psi(A,B)$
→ 만약 $\psi(A,B) = P(A,B)$로 두면 $A$에 대해서 marginalization을 진행하게 되면 $P(B)$가 자연스럽게 나옴. - $P(B) = \sum_C \psi(B,C)$
→ 위와 동일하게 $C$에 대해서 marginalization을 진행하게 되면 $C$를 이용해 $P(B)$를 만들 수 있음. - $P(B) = \phi(B)$
→ 이건 Seperator에 대한 notation으로 얻을 수 있는 값. - How to find out the $\psi$s and the $\phi$s?
- When the $\psi$s cahnge by the observations: $P(A,B)$ → $P(A-1, B)$
- A single $\psi$ change can result in the change of multiple $\psi$s
- The effect of the observation propagates through the clique graph Belief propagation
- 즉, Observation에 의해서 Potential Graph 원소 값이 변화했을 때, 해당 Observation의 결과가 Clique graph의 개형에 의해서 “전파”됨. 이러한 과정을 Belief propagation이라고 함
- $P(B) = \sum_A \psi(A,B)$
- How to propagate the belief?
- Absorption (update) rule
- Assume $\psi^*(A,B), \psi(B,C)$ and $\phi(B)$
- → $\psi$의 함수가 개형이 $\psi^$로 변화했다면, 나머지 함수들도 그래프 개형에 의거해 영향이 있다면 수정을 해야함. 이를 위에서 언급한 Absorption Rule을 통해서 진행함.**
- Define the update rule for separators
- $\phi^(B) = \sum_A\psi^(A,B)$
→ Observation에 의거해 변화하는 Random Variable에 대해서 Marginalization 과정을 진행하면 쉽게 알아낼 수 있음.
- $\phi^(B) = \sum_A\psi^(A,B)$
- Define the update rule for cliques
- $\psi^(B,C) = \psi(B,C)\frac{\phi^(B)}{\phi(B)}$
→새로 만들어진 Potential Function은 이전에 알아냈던 Potential Function에 새로 알아낸 Seperator를 예전 것으로 나눈 것의 곱으로 표현 가능하다고 합니다. - Why does this work?
- $\sum_C \psi^(B,C) = \sum_C \psi(B,C) \frac{\phi^(B)}{\phi(B)}
\
= \frac{\phi^(B)}{\phi(B)}\sum_C \psi(B,C)= \frac{\phi^(B)}{\phi(B)}\phi(B) = \sum_A \psi^*(A,B)$- 위에서 $P(B) = \sum_A \psi(A,B) = \sum_C \psi(B,C) = \phi(B)$를 유지하면서 $\psi(A,B)$를 update하는 것에서 착안해서 증명합니다.
- 그냥 결론을 “옳다”고 생각하고 식을 전개하면 $\sum_C \psi(B,C) \frac{\phi^(B)}{\phi(B)}$ 가 되는데, $\frac{\phi^(B)}{\phi(B)}$ 해당 파트는 $C$과 연관이 없으므로 앞으로 옮겨올 수 있습니다. 남은 $\sum_C \psi(B,C)$ 부분은 $P(B)$와 동일하게 되고, $P(B) = \phi(B)$와 동일합니다. 고로 남은 파트는 $\phi^_(B)$인데, 해당 부분은 Observation한 부분이므로, $A$에 대해서 Marginalization을 진행한 것과 같아 $\sum_A \psi^_P(A,B)$로 표현가능합니다. 즉, 우리가 처음에 의도했던 가정을 지키는 것과 동일하게 되므로 이런식으로 update를 할 수도 있다는 뜻이 됩니다.
- Guarantess the local consistency
→ Global consistency after iterations
- $\sum_C \psi^(B,C) = \sum_C \psi(B,C) \frac{\phi^(B)}{\phi(B)}
- $\psi^(B,C) = \psi(B,C)\frac{\phi^(B)}{\phi(B)}$
7.9 Simple Example of Belief Propagation
Simple Example of Belief Propagation


- Initialized the potetntial functions위와 같은 그래프 개형에서의 Potential Grpah인 $\psi$는 위와 같이 나올 수 있습니다.

- Example 1. $P(b) = ?$
- 먼저 이 질문이 나오게 된 이유는 우리가 직접적으로 $P(b)$를 구할 수 없기 때문.
- 아마 $P(b)$를 구하기 위해 probability table을 직접 만들어서 구하려고 할 텐데, 사실 이렇게 graphical 하게 Network가 연결되어 있다면 parents로부터 “영향”을 받을 수 밖에 없고, 이는 곧 conditional probability밖에 없지 못하는 것을 의미합니다. 고로 우리는 $P(B|C)$ 혹은 $P(A|B)$밖에 구할 수 없으므로 $P(b)$는 무엇인가에 대한 질문이 나오게 됩니다.먼저 이 질문이 나오게 된 이유는 우리가 직접적으로 $P(b)$를 구할 수 없기 때문.
- 위의 유도 과정은 다음과 같습니다.
- $\phi^*(b)$와 absortion rule을 이용해 알아보면 될 것 같습니다.
- $\sum_a \psi(a,b) = 1$
→ 이는 곧 a의 모든 사건에 대해서 marginalization을 해야함을 의미하므로 전체 확률인 1을 의미합니다. 그리고 1이 나오게 되는 이유는 우리가 $\psi(a,b) = P(a|b)$로 뒀기 때문입니다.
현재 이 과정은 Belief Propagation으로 $P(b)$가 Observation을 통해 변화했을 때 다른 node의 확률이 어떻게 변화하는지를 살펴보고 있는 것입니다. - $\psi^(b,c) = \psi(b,c)\frac{\phi^(b)}{\phi(b)} = P(b|c)P(c) = P(b,c)$
→ Belief Propagation 과정 중으로 바뀐 Potential Function $\phi^(b)$에 의거해 Potential Funciton인 $\psi^(b,c)$가 어떻게 변화하는지 유도하는 식입니다.
기존의 $\psi(b,c) = P(b|c)P(c)$였고 현재도 $\frac{\phi^(b)}{\phi(b)} = 1$이므로 변화하지 않았습니다. 그래도 $b,c$의 joint probability입니다.
즉 Clique Graph의 그림상에서 $B$를 update했고, Clique인 $B,C$를 Belief Propagation 과정을 통해 Update를 했습니다. 이후에는 Network의 구조에 따라 $B$ 혹은 $B,C$를 paraents로 가지는 Clique를 Update를 할 차례입니다.
이제 Clique $B, C$를 update했으니 $B$를 Clique $B,C$를 Marginalize output을 이용해 $\phi^(b)$가 나와야 할텐데 하지만 나오지 않습니다. 왜냐하면 Clique $A,B$는 conditional probability Table로 초기 setup이 되어 있지만. Clique $B,C$는 joint probability로 되어있기 때문에 local structure가 맞지 않는 상태입니다. 고로 Clique $B,C$로부터 다시 Belief Propagation을 진행해 Local Consistency를 유지해야하는 상황입니다. - $\phi^{}(b) = \sum_c\psi(b,c) = \sum_cP(b,c) = P(b)$
→ $C$에 대해서 marginalization을 진행하게 되면 새로운 Potential Function인 $\phi^{}(b)$가 나옴. 이것을 이용해 이제 Clique $A,B$를 Update 할 예정 - $\psi^(a,b) = \psi(a,b)\frac{\phi^{**}(B)}{\phi^(b)} = \frac{P(a|b)P(b)}{1} = P(a,b)$
→ 3으로 얻은 $\phi^{*}(b)$를 이용해 이전의 $\phi^(b)$(근데, 내 생각엔 사실 $\phi(b)$가 되어야 할 것 같긴한데, 값이 같으니 같은 의미를 하는 것이라 생각)을 이용해 Belief Propagation을 진행해 Clief $A,B$를 update하고 해당 값을 얻는 과정. - $\phi^{}(b) = \sum_a\psi^(a,b) = P(b)$
→ 새로이 Observation을 해서 새로운 Potential Function인 $\phi^{*}(b)$를 얻었을 때 해당 값은 이전에 Potential Function의 결과랑 같으므로 동일하게 과정이 진행되므로, Local Consistency가 maintain하게 됩니다.
- Most Probable Assignment problem을 푸는 conditional probability가 될 것이다. 즉, 관측이 있는 상황(evidence)가 있는 상황에서 우리가 알지 못하지만 관심이 있는 hidden variable에 대해서 구하려고 하는 상황
- 먼저 이 질문이 나오게 된 이유는 우리가 직접적으로 $P(b)$를 구할 수 없기 때문.

- Example2. $P(b|a = 1, c=1) = ?$
→ 새로운 evidence, $a=1, c=1$인 상황에서의 $P(b)$를 구하는 상황.- $\phi^(b) = \sum_a\psi(a,b)\delta(a=1) = P(a=1|b)$
→ $\delta(a=1)$이라는 term을 사용해 “우리는 $a=1$인 상황만을 marginalize Out하겠다”라는 뜻입니다. 그래서 새로이 $\phi^(b)$ 가 $P(a=1
|b)$로써 정의가 되는 것입니다. - 그 외의 과정은 Example1과 같이 동일하게 진행되고 최종적으로 $\phi^{}(b)$와 $\phi^{*}(b)$가 동일한 값을 가지게 되기 때문에 local consistency가 maintain되고 있다고 볼 수 있습니다.
- $\phi^(b) = \sum_a\psi(a,b)\delta(a=1) = P(a=1|b)$
정리
- Clique (클릭): 그래프에서 모든 노드가 서로 직접 연결되어 있는 노드의 집합을 의미합니다. 즉, 클릭 내의 모든 노드 쌍 사이에는 간선이 있어야 합니다.
- Separator (세퍼레이터): 그래프를 두 개 이상의 연결되지 않은 부분 그래프로 나누는 노드의 집합을 의미합니다. 세퍼레이터는 그래프의 연결성을 끊어서 두 개 이상의 독립적인 부분 그래프로 나누는 역할을 합니다.
예를 들어, 그래프에서 A, B, C 세 노드가 모두 서로 연결되어 있다면 {A, B, C}는 클릭입니다. 그러나 만약 A와 B 사이의 간선을 제거하면, A는 {B, C}와 {A}를 분리하는 세퍼레이터 역할을 합니다.
따라서, 클릭과 세퍼레이터는 다른 개념이지만, 특정 상황에서는 클릭이 세퍼레이터 역할을 할 수도 있습니다. 그러나 일반적으로 두 개념은 서로 다릅니다.
7장 Quiz
1번 문제
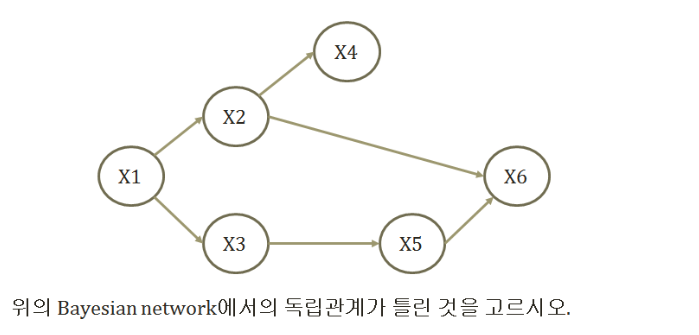
DAG에서 각 노드의 연결 상태는 크게 3가지로 나타낼 수 있습니다.
- Common parent
- $J \bot M|A$ → A에 대한 정보가 있을 때, $J$와 $M$은 independent하다.
- $P(J, M|A) = P(J|A)P(M|A)$
- Cascading
- $B\bot M|A$ → A에 대한 정보가 있을 때 $B$와 $M$은 independent하다.
- $P(M|B,A) = P(M|A)$
- V-Structure
- $\sim (B\bot E|A)$ -> A에 대한 정보가 있으면 $B$와 $E$은 dependent하다
- $P(B,E,A) = P(B)P(E)P(A|B,E)$
각각의 상태에 대한 Fiagure는 다음과 같습니다.


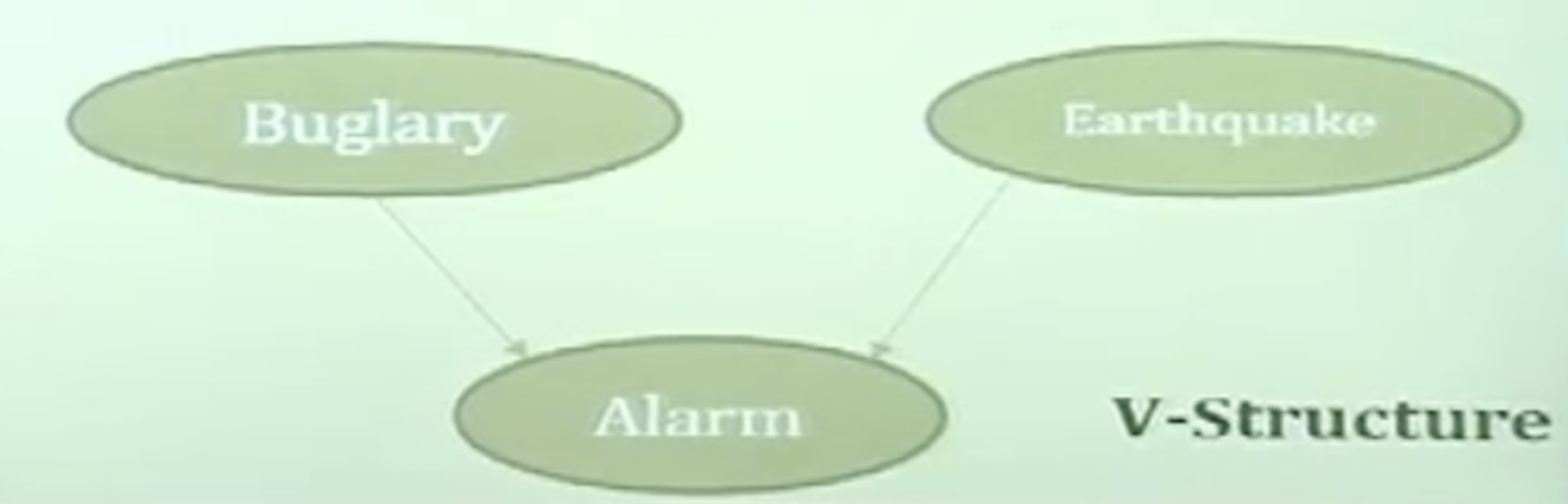
이것을 잘생각하면서 보기를 읽고 해결하면 됩니다.
2번 문제

$P(Alarm=T)$인 값을 구하기 위해서는 Alarm = T에 대해서 나머지 Random Variable을 Marginalization하는 과정이 필요합니다.
현재 우리가 가지고 있는 Random Variable이 B(Buglary)와 E(Earthquake)가 있으므로 $\sum_{B}sum_{E}P(Alarm=T, B, E)$를 구하면 됩니다. 이때 현재 DAG의 개형이 V-Structure이므로,. 우리는 $P(B,E,A) = P(B)P(E)P(A|B,E)$라는 식을 이용할 수 있습니다. 해당 식과 주어진 Probability Table을 이용한다면 값을 계산할 수 있습니다.
3번 문제

$P(Alarm=T| J=T, M=T)$인 값을 구하기 위해서는 Alarm = T에 대해서 나머지 Random Variable을 Marginalization하는 과정이 필요합니다. 선행적으로 알아야 할 것은 Graph의 개형이 Common Parents입니다. $P(J, M|A) = P(J|A)P(M|A)$라는 것을 알고 있어야 합니다. 이제 주어진 식 $P(Alarm=T| J=T, M=T)$를 다음과 같이 변환해 보겠습니다.
$$P(Alarm=T| J=T, M=T) = \cfrac{P(J=T, M=T|A=T)P(A=T)P(A=T)}{P(J=T, M=T)}$$
여기서 $P(J=T, M=T|A=T) = P(J|A)P(M|A)$입니다. 이는 Probability Table에 잘 나와있고, $P(A=T)$ 인경우도 잘 나와있습니다. 이제 중요한 것은 $P(J=T, M=T)$ 인 경우입니다. 이는 Random Variable인 $A$를 Marginalization 하면 됩니다.
즉, $\sum_{A}P(J= T, M=T,A=T)$를 수행하면 얻을 수 있습니다.
위의 과정을 모두 수행하면 정답을 맞출 수 있습니다.
'DeepLearning > 인공지능 개론' 카테고리의 다른 글
| 인공지능 및 기계학습 개론 2(8.4~8.5) 정리 (5) | 2023.10.15 |
|---|---|
| 인공지능 및 기계학습 개론 2(8.1~8.3) 정리 (1) | 2023.10.14 |
| 인공지능 및 기계학습 개론 2(7.4~7.6) 정리 (1) | 2023.10.02 |
| 인공지능 및 기계학습 개론 2(7.1~7.3) 정리 (0) | 2023.10.01 |





